
골드 Ⅳ
https://www.acmicpc.net/problem/15685
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커
www.acmicpc.net
📄 문제
- 드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다.
- 시작 점
- 시작 방향
- 세대
- 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
- K(K > 1) 세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
- 크기가 100×100인 격자 위에 드래곤 커브가 N개 있다.
- 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
- 방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.
- 0: x좌표가 증가하는 방향 (→)
- 1: y좌표가 감소하는 방향 (↑)
- 2: x좌표가 감소하는 방향 (←)
- 3: y좌표가 증가하는 방향 (↓)
이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오.
예시
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.
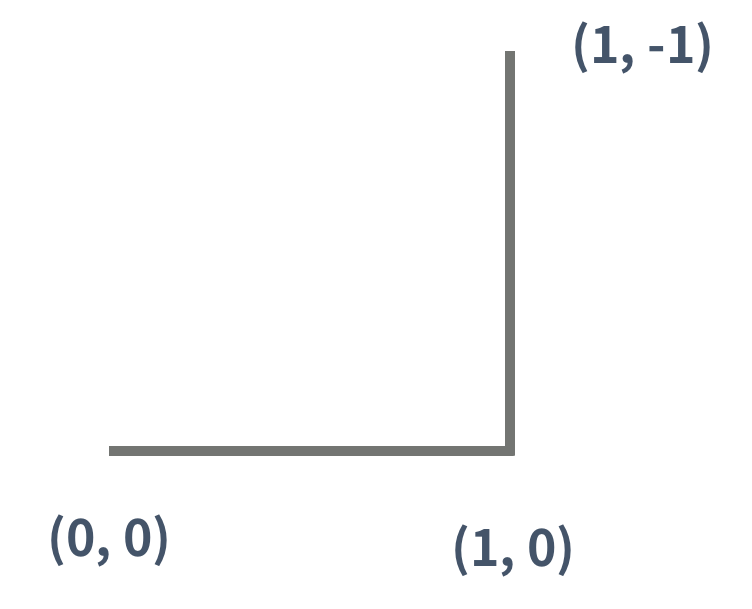
2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)

3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.

💡 아이디어
- 주어진 문제의 순서에 따라 구현하는 시뮬레이션 문제이다.
- 0세대부터 g세대까지 드래곤 커브가 추가된다.
- 0세대는 주어진 인풋값 그대로 이동하여 선분을 그린다..

- 현재 세대는 이전 세대의 그래프(선분들)를 시계 방향으로 90도 회전한 모양을 끝점에 추가한 모양이다.



- 따라서, 다음 세대에 그려질 선분들의 위치와 방향을 구하기 위해 현재 세대 선분들의 이동 방향을 저장해야 한다.
- 이전 세대의 끝점에서 시작하여 이전 세대 끝 선분부터 이동 방향을 각각 시계방향으로 90도 회전하며 이어 붙인다.
- 즉, 0세대부터 g세대까지 첫 이동 방향부터 세대를 거듭하며 추가되는 각 세대 선분들의 이동 방향을 갱신하는 함수가 필요하다.
- 또한, 이후 정사각형의 개수를 찾기 위해 0세대부터 g세대까지의 선분을 잇는 점의 위치도 저장해야 한다.
- 이동 방향을 저장하면서 이동한 위치도 함께 저장해 주면 된다.
- 마지막으로, 모든 위치가 저장된 그래프에서 길이가 1인 정사각형의 개수를 찾는 함수가 필요하다.
- 즉, 길이가 1인 정사각형을 이루는 4개의 점에 모두 방문했는지 판단해야 한다.
- 정사각형을 이루는 4개의 점이 존재한다면 개수도 함께 세어준다.
- 존재하는 정사각형의 개수를 출력한다.
1. 각 세대 선분들의 이동 방향을 갱신하는 함수 (dragon_curve)
- 우선 문제에서 주어진 인풋값을 활용하여 초기 설정을 한다.
- 이동 방향들을 저장할 배열(move)을 만들어 준다.
- 이동 방향 d를 이동 방향들을 저장할 배열(move)에 넣어준다
- graph에 시작 값과 d방향으로 이동한 위치를 방문 체크한다. (0세대)
- 각 세대의 끝점을 저장할 변수를 0세대의 끝점으로 초기화하여 생성한다.
- 1세대부터 g세대까지의 방향과 이동 위치를 구한다.
- 이 함수에서 가장 중요한 부분은 끝 점을 기준으로 90도 시계 방향 회전 시킨 모양을 구하는 방법을 구현하는 것이다.
- 방향을 설정하고 새로운 위치 값을 구해준다.
- 새로운 위치 값이 격자의 범위 안에 들어오는지 확인한다.
- 들어오면, graph에 방문 체크를 하고 이동 방향을 저장하는 배열(move)에 이동한 방향을 추가한다.
- 이동된 점을 끝점으로 갱신한다.
문제 그림을 예시로 세대 간의 방향 변화를 설명하면,
이동 방향 d는 아래와 같이 변화한다.
| 0 세대 | 0 | |||||||
| 1 세대 | 0 | 1 | ||||||
| 2 세대 | 0 | 1 | 2 | 1 | ||||
| 3 세대 | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 1 |
즉, 다음 세대의 이동 방향은 이전 세대의 이동 방향을 뒤에서부터 순차적으로 +1을 한 값이다. ( (move[k] + 1) % 4 )
2. 방문한 모든 점의 위치가 저장된 그래프에서 길이가 1인 정사각형의 개수를 찾는 함수 (find_square)
- 모든 점을 방문 체크한 2차원 배열 graph를 정사각형 모양으로 탐색한다.
- 정사각형 모양의 점에 모두 방문했을 경우 정사각형 개수를 추가해 준다.
📝 문제 풀이 (Code)
import sys
input = sys.stdin.readline
# 각 세대의 이동 방향과 마지막 위치를 저장 함수
def dragon_curve():
global last_i, last_j, move
# 이전 세대의 끝점을 다음 세대의 시작점으로 갱신
# 끝 점을 기준으로 90도 시계 방향 회전시킨 선분의 방향을 순서대로 추가한다.
m = len(move)
for k in range(m-1, -1, -1):
# k값 0, 1, 2, 3으로 나오게 변경
z = (move[k] + 1) % 4
# 변경된 위치값
ni = last_i + di[z]
nj = last_j + dj[z]
if 0 <= ni <= 100 and 0 <= nj <= 100:
# 방문 체크
graph[ni][nj] = 1
# 이동 방향을 추가로 저장
move.append(z)
last_i = ni
last_j = nj
# 정사각형이 몇개인지 찾는 함수
def find_square():
cnt = 0
for r in range(100):
for c in range(100):
# 정사각형 이면
if graph[r][c] and graph[r + 1][c] and graph[r][c + 1] and graph[r + 1][c + 1]:
cnt += 1
return cnt
n = int(input())
graph = [[0] * 101 for _ in range(101)]
# 동북서남
di = [0, -1, 0, 1]
dj = [1, 0, -1, 0]
# x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대
for _ in range(n):
# x축(열) = j, y축(행) = i
j, i, d, g = map(int, input().split())
# 시작점 방문 체크
graph[i][j] = 1
# 이동 방향 저장
move = [d]
# 0세대 이동 위치
last_i = i + di[d]
last_j = j + dj[d]
# 이동 방문 체크
graph[last_i][last_j] = 1
# g번 반복 (1세대부터 g세대까지)
for _ in range(g):
# 끝 점을 기준으로 90도 시계 방향 회전 시킨 모양의 위치와 방향을 추가하는 함수
dragon_curve()
# 정사각형의 개수 찾기
print(find_square())'Algorithm Solving > Baekjoon' 카테고리의 다른 글
| [백준] 7662 이중 우선순위 큐 (파이썬) (0) | 2023.09.12 |
|---|---|
| [백준] 1300 K번째 수 (파이썬) (0) | 2023.09.11 |
| [백준] 12100 2048 (Easy) (파이썬) (0) | 2023.09.06 |
| [백준] 2668 숫자고르기 (파이썬) (0) | 2023.09.05 |
| [백준] 20437 문자열 게임 2 (파이썬) (0) | 2023.09.04 |