최장 증가 부분 수열(Longest Increasing Subsequence)이란?
원소개 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대인 부분 수열을 최장 증가 부분 수열이라고 한다.
간단히 말해, 가장 긴 증가하는 부분 수열이다.
예시
[6, 2, 5, 1, 7, 4, 8, 3] 이라는 배열에서 최장 증가 부분 수열(LIS)은 [2, 5, 7, 8]이 된다.
[2, 5, 7], [2, 4, 8] 등 증가하는 부분 수열은 많지만 그 중에서 가장 긴 것은 [2, 5, 7, 8]이다.
최장 증가 부분 수열 알고리즘 풀이 방법
최장 증가 부분 수열의 길이를 구할 수 있는 풀이 방법은 크게 2가지가 있다.
- 동적계획법 (DP, Dynamic Programming)
- 이분 탐색 (Binary Search)
LIS를 해결하기 위한 가장 일반적이고 간편한 방법은 DP를 이용하는 것이다.
DP(Dynamic Programming) 문제로 자주 출제된다.
1. 동적계획법(Dynamic Programming)을 활용한 풀이 유형
- 시간복잡도: O(n^2)
- 인풋 값이 1,000,000개 정도만 되어도 O(n^2)의 알고리즘은 실행시간이 10초 이상 소요된다고 알려져 있다.
- 따라서, DP를 이용한 방법은 분명 완전 탐색에 비해 시간 복잡도 면에서 효율적이지만, 여전히 시간복잡도가 O(n^2)이라는 점 비효율적이다.
동작 방법
- 수열의 길이와 같은 dp배열을 하나 선언한다. dp배열은 부분 수열의 길이가 담는다.
- 각 수는 자기자신인 1개의 수를 최소 길이로 가진다. 따라서, dp 배열은 1로 초기화하여 생성한다.
- 수열을 처음부터 끝까지 순서대로 1개씩 탐색한다. ( 현재 위치 = i )
- 맨 앞 수는 자기자신 하나이므로 for 문을 활용하여 두 번째 수부터 탐색한다. ( range(1, len(array)) )
- for문으로 현재 위치의 수와 이전 위치의 수들을 차례대로 비교한다.
- 현재 위치(i)가 앞에 있는 원소(j)들 보다 큰지 체크한다.
- 현재 위치(i)가 앞에 있는 원소(j)들 보다 더 크면(증가하면) dp[j]+1과 dp[i]를 비교하여 dp[i]을 더 큰 값으로 변경한다.
- dp[j]+1 : j 위치에 저장된 수열에 i를 추가하여 개수를 1개 증가 시켜 저장해준다.
- dp[i] : 현재 i 위치에 저장되어있는 수열의 길이이다.
- dp배열의 원소 중에서 가장 큰 값을 출력하면 최장 증가 부분 수열의 길이가 된다.
예시
array = [7, 2, 1, 4, 5, 3]가 있다.
먼저 dp[0]의 값은 1로 초기화 해준다. 자기 자신 하나는 무조건 수열로 가지고 있기때문에 증가 부분 수열의 길이는 모두 1부터 시작한다.
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| array | 7 | 2 | 1 | 4 | 5 | 3 |
| dp | 1 |
다음으로 array[1]을 살펴보자. 앞의 array의 값(array[0])과 비교했을 때 작으므로 dp[1]에는 1이 들어간다.
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| array | 7 | 2 | 1 | 4 | 5 | 3 |
| dp | 1 | 1 |
array[2] 역시 앞의 array 값들과 비교했을 때 작으므로 dp[2]에는 1이 들어간다.
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| array | 7 | 2 | 1 | 4 | 5 | 3 |
| dp | 1 | 1 | 1 |
array[3]은 array[1]과 array[2]에 비해 큰 값이다.
dp[1]과 dp[2]는 값이 1로 같으므로 dp[3]에는 1 + 1인 2가 들어가게 된다.
- dp[3] = max(dp[3], dp[1] + 1) = 2
- dp[3] = max(dp[3], dp[2] + 1) = 2
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| array | 7 | 2 | 1 | 4 | 5 | 3 |
| dp | 1 | 1 | 1 | 2 |
array[4]는 array[1], array[2], array[3]에 비해 큰 값이다.
dp[1]과 dp[2]는 값이 1로 같아 1 + 1인 2가 들어가게 되지만 dp[3]은 2이므로 2 + 1인 3이 들어가게 된다.
따라서, 이 중 dp[3]이 2로 가장 큰 값이므로 dp[4]에는 2 + 1인 3이 들어가게 된다.
- dp[4] = max(dp[4], dp[1] + 1) = 2
- dp[4] = max(dp[4], dp[2] + 1) = 2
- dp[4] = max(dp[4], dp[3] + 1) = 3
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| array | 7 | 2 | 1 | 4 | 5 | 3 |
| dp | 1 | 1 | 1 | 2 | 3 |
마지막 array[5]는 array[1], array[2]에 비해 큰 값이다.
dp[1]과 dp[2]는 값이 1로 같으므로 dp[5]에는 1 + 1인 2가 들어가게 된다.
- dp[5] = max(dp[5], dp[1] + 1) = 2
- dp[5] = max(dp[5], dp[2] + 1) = 2
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 |
| array | 7 | 2 | 1 | 4 | 5 | 3 |
| dp | 1 | 1 | 1 | 2 | 3 | 2 |
이렇게 만들 수 있는 모든 부분 증가 수열의 길이를 구하였다. 이중 LIS의 길이는 dp배열에서 가장 큰 값에 해당하는 3이 된다.
LIS 소스코드 : 파이썬 (Python)
1. DP로 구현한 최장 증가 부분 수열 알고리즘
# 수열 array
array = [6, 2, 5, 1, 7, 4, 8, 3]
# 다이나믹 프로그래밍을 위한 1차원 DP 테이블 초기화
# dp에는 수열의 길이를 담는다.
dp = [1] * n
# 가장 긴 증가하는 부분 수열(LIS) 알고리즘 수행
# 맨 앞은 수열이 자기자신 1개이기 때문에 두 번째 수 부터 비교한다.
for i in range(1, n):
# array의 i번째 앞에 수들을 비교한다.
# 처음부터 i-1번째 인덱스까지 i번째 수와 비교
for j in range(i):
# 숫자의 크기를 비교하여 증가하면
if array[j] < array[i]:
# 이전 길이에 +1한 값과 저장된 값을 비교하여 더 큰 값으로 변경
# dp 배열의 값을 더 큰 값으로 갱신
dp[i] = max(dp[i], dp[j] + 1)
# LIS의 길이는 dp에서 가장 큰 값을 의미한다.
answer = max(dp)
2. 이분 탐색(Binary Search)을 활용한 풀이 유형
DP를 이용한 방법은 분명 완전 탐색에 비해 시간 복잡도 면에서 효율적이지만, 여전히 O(N^2)이라는 점이 발목을 잡는다.
이 때, 이분 탐색(Binary Search)을 사용하면 시간 복잡도를 O(NlogN)으로 줄일 수 있다.
- 시간복잡도: O(nlog n)
- LIS의 형태를 유지하기 위해 주어진 배열의 인덱스를 하나씩 살펴보면서 그 숫자가 들어갈 위치를 이분 탐색으로 찾아서 넣는다.
- 이분탐색은 일반적으로 시간복잡도가 O(log n)으로 알려져있기 때문에 이분탐색을 활용한 LIS의 길이 구하기의 시간복잡도는 O(nlog n)이다.
- 이분 탐색(Binary Search)을 이용한 방법은 LIS를 기록하는 배열을 하나 더 두고, 원래 수열에서의 각 원소에 대해 LIS 배열 내에서의 위치를 찾는다.
예시1

예시2




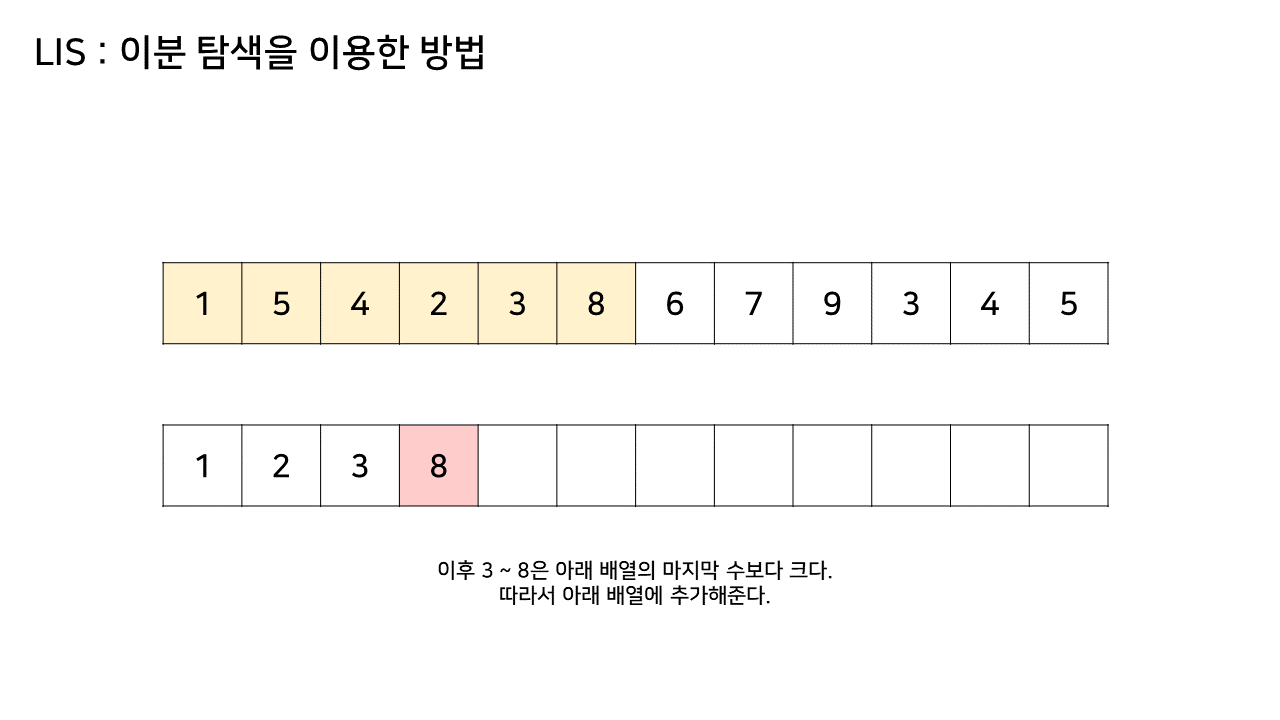
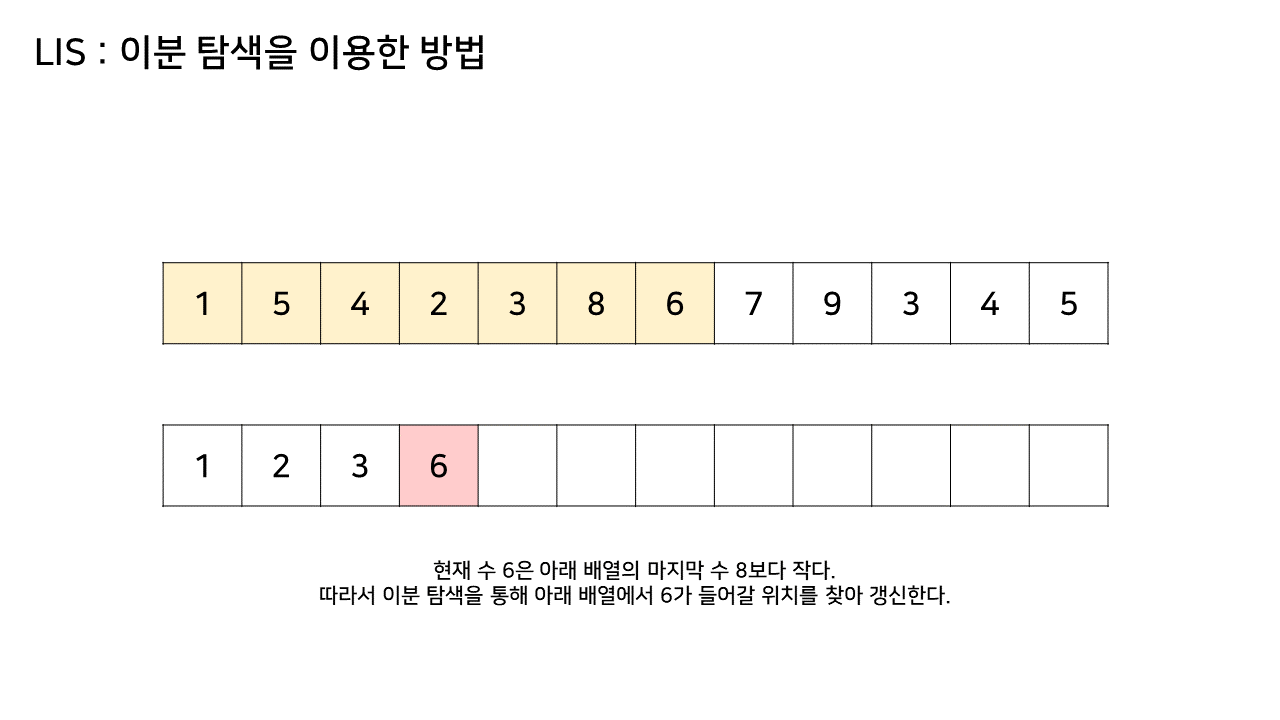

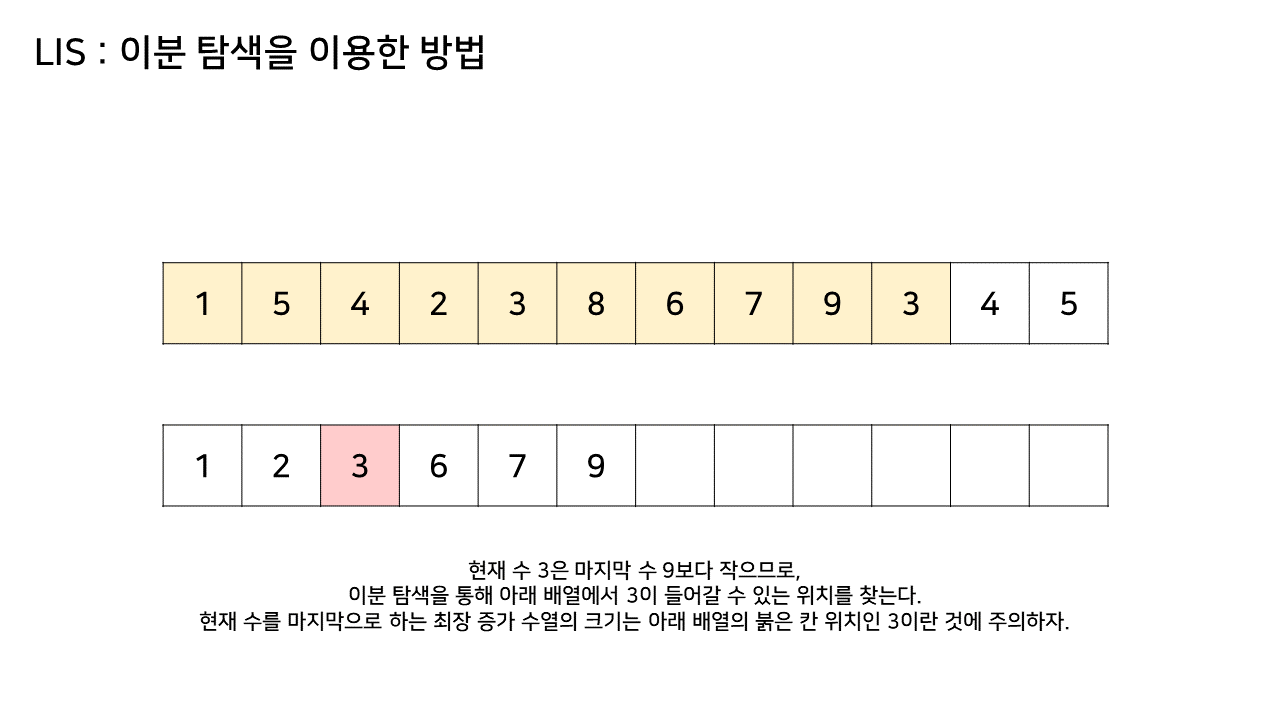

그림의 아래 배열의 크기는 최대 6까지 갔었으므로, LIS의 길이는 6이 된다.
이 방법은 그림의 아래 배열을 LIS의 형태로 유지하기 위해, 기존 수열의 각 원소가 LIS에 들어갈 위치를 찾는 원리로 동작한다.
즉, 현재 원소를 아래 배열에 넣어 LIS를 유지하려고 할 때, 그 최적의 위치를 찾는 것이다.
동작 방법
- 증가하는 부분 수열을 담을 lis 배열을 선언한다.
- 주어진 array 수열의 첫 번째 값을 lis 배열에 담은 상태로 초기화를 하고 시작한다.
- array 수열의 두 번째 값(target)부터 마지막 target 값까지를 lis 배열의 마지막 값과 비교하여
- 마지막 값보다 target 값이 더 크다면 lis 배열의 마지막에 target 값을 추가하고,
- 마지막 값보다 target 값이 더 작다면 이분탐색을 통해 lis 배열 값 중 target 값보다 크면서 제일 작은 값의 위치를 찾아 target 값으로 갱신한다.
- array 배열에 대한 모든 탐색이 끝나고, lis 배열의 길이를 구하면 최장 증가 부분 수열의 길이가 된다.
LIS 소스코드 : 파이썬 (Python)
2. 이분 탐색으로 구현한 최장 증가 부분 수열 알고리즘
# LIS의 길이를 유지하기 위해 숫자가 들어갈 위치를 이분탐색으로 찾는 함수
def binary_search(target, lis):
# 초기 시작점과 끝점 설정
start = 0
end = len(lis) - 1
# target 값과 같거나 큰 수 중 가장 작은 값을 찾아야 하기 때문에 일반 이분 탐색과는 조건이 살짝 다르다.
# lis 배열에 들어갈 target 순서의 위치를 이분탐색으로 찾기
# 같은 값만을 찾는 것이 아니기 때문에 마지막 2개가 남았을때도 비교 해야하므로 start <= end가 아니다.
while start < end:
# 중간값
mid = (start + end) // 2
# 중간값이 타겟과 같다면 중간값의 위치를 반환
if lis[mid] == target:
return mid
# target이 더 작으면 왼쪽 더 탐색
elif lis[mid] > target:
end = mid
# target이 더 크면 오른쪽 더 탐색
else:
start = mid + 1
return endarray = [5, 2, 1, 4, 3, 5]
lis = [array[0]] # A 수열의 첫번째 값
# array 수열의 두번째 값부터 LIS의 마지막 값과 비교
for i in range(1,n):
# 현재 비교 대상 값(target)
target = array[i]
# 현재 값(target)이 lis 배열의 마지막 값보다 클 경우 LIS 배열에 추가
if lis[-1] < target:
lis.append(target)
# 현재 값(target)이 더 작다면 이분탐색을 통해 LIS 배열 갱신
# 현재 값이 lis 배열의 몇 번째 인덱스(idx)에 들어갈 수 있는지를 찾아서
# lis 배열의 idx 위치에 값을 현재 값으로 변경해준다.
else:
idx = binary_search(target, lis)
lis[idx] = target
# 최종 LIS 길이 반환
return len(lis)
참고자료
https://4legs-study.tistory.com/106
https://one10004.tistory.com/217
https://code-angie.tistory.com/2
'Algorithm' 카테고리의 다른 글
| [알고리즘] 서로소 집합 (Disjoint Sets) - 사이클 판별 (0) | 2023.12.10 |
|---|---|
| [알고리즘] 서로소 집합 (Disjoint Sets) - 자료구조 (0) | 2023.12.09 |
| [알고리즘] 에라토스테네스의 체 (소수 판별) (0) | 2023.08.25 |
| [알고리즘] 이진 탐색 / 이분 탐색 (Binary Search) (0) | 2023.08.17 |
| [알고리즘] 시간 복잡도 (Time Complexity) (0) | 2023.08.14 |