소수 (Prime Number)
1보다 큰 자연수 중에서 1과 자기 자신을 제외한 자연수로는 나누어 떨어지지 않는 자연수
- 6은 1, 2, 3, 6으로 나누어 떨어지므로 소수가 아니다.
- 7은 1과 7을 제외하고는 나누어 떨어지지 않으므로 소수이다.
소수의 판별: 기본적인 알고리즘
1. 기본적인 알고리즘 소스 코드- 파이썬 (Python)
# 소수 판별 함수 (2이상의 자연수에 대하여)
def is_prime_number(x):
# 2부터 (x - 1)까지의 모든 수를 확인하며
for i in range(2, x):
# x가 해당 수로 나누어 떨어진다면
if x % i == 0:
return False # 소수가 아니다.
# 나누어 떨어지는 수가 하나도 존재하지 않는다면
return True # 소수이다.
print(is_prime_number(4))
print(is_prime_number(7))실행 결과
>>> False
# 4가 소수이니? False
>>> True
# 7이 소수이니? True2. 기본적인 알고리즘 성능 분석
- X가 주어졌을 때 X를 2부터 X - 1까지의 모든 자연수로 나누어 본다.
- 만약 2부터 X-1까지의 모든 자연수로 나누었을 때
- 나누어 떨어지는 수가 하나라도 존재하면 False를 반환하며 X는 소수가 아니다.
- 나누어 떨어지는 수가 존재하지 않으면 True를 반환하며 X는 소수이다.
2부터 X-1까지의 모든 자연수에 대하여 연산을 수행해야 한다.
따라서, 모든 수를 하나씩 확인한다는 점에서 시간 복잡도는 O(X)이다.
예를 들어,
1,000,000이라는 수가 소수인지 판별하려면 1,000,000을 2부터 999,999까지의 모든 수에 대하여 하나씩 나누어야 한다.
즉, 소수인지 판별이 필요한 수를 n이라고 하면 시간 복잡도가 O(n)이기에 매우 비효율적이다.
위의 알고리즘을 개선하기위해 약수의 성질을 이용한다.
약수 (Divisor)
어떤 수를 나누어 떨어지게 하는 0이 아닌 정수
- 1은 모든 수의 약수이고, 자기 자신도 약수이다.
- 어떤 수도 0으로 나눌 수 없기 때문에 0은 어떤 수의 약수도 아니다.
약수의 성질
예를 들어 16이라는 수의 약수는 다음과 같다.
- 1 X 16 = 16
- 2 X 8 = 16
- 4 X 4 = 16
- 8 X 2 = 16
- 16 X 1 = 16

- 모든 약수가 가운데 약수를 기준으로 곱셈 연산에 대해 대칭을 이루는 것을 알 수 있다.
- 예를 들어, 16의 약수는 1, 2, 4, 8, 16이다.
- 이때, 2 X 8 = 16은 8 X 2 = 16과 대칭이다.
- 따라서, 특정한 자연수 X가 소수인지 확인하기 위해 가운데 약수까지만 '나누어 떨어지는지' 확인하면 된다.
- 즉, 특정한 자연수의 모든 약수를 찾을 때 제곱근(가운데 약수)까지만 확인하면 된다.
- 예를 들어, 16이 2로 나누어 떨어진다는 것은 8로도 나누어 떨어진다는 것을 의미한다.
소수의 판별: 개선된 알고리즘
1. 개선된 알고리즘 소스 코드: 파이썬 (Python)
import math
# 소수 판별 함수 (2이상의 자연수에 대하여)
def is_prime_number(x):
# 2부터 x의 제곱근까지의 모든 수를 확인하며
for i in range(2, int(math.sqrt(x)) + 1):
# x가 해당 수로 나누어 떨어진다면
if x % i == 0:
return False # 소수가 아니다.
# 나누어떨어지는 수가 하나도 존재하지 않는다면 소수이다.
return True # 소수이다.
print(is_prime_number(4))
print(is_prime_number(7))실행 결과
>>> False
# 4가 소수이니? False
>>> True
# 7이 소수이니? True2. 개선된 알고리즘 성능 분석
- X가 주어졌을 때 X를 2부터 X의 제곱근까지의 모든 자연수로 나누어 본다.
- 만약 2부터 X의 제곱근까지의 모든 자연수로 나누었을 때
- 나누어떨어지는 수가 하나라도 존재하면 False를 반환하며 X는 소수가 아니다.
- 나누어떨어지는 수가 존재하지 않으면 True를 반환하며 X는 소수이다.
2부터 X의 제곱근(소수점 이하 무시)까지의 모든 자연수에 대하여 연산을 수행해야 한다.
따라서, 시간 복잡도는 O(X½)이다.
개선된 소수 판별 알고리즘의 시간 복잡도는 제곱근까지만 확인하면 되기 때문에 시간 복잡도가 O(N½)이 된다.
그런데 만약 소수인지 아닌지 판별해야 되는 수가 1,000,000일 때는 위의 알고리즘으로 모든 수를 하나씩 검사하는 것으로는 느릴 수 있다.
하나의 수에 대해서 소수인지 아닌지 판별하는 방법을 알아보았다.
하지만 특정한 수의 범위 안에 존재하는 모든 소수를 찾아야 할 때는 어떻게 할까?
에라토스테네스의 체 알고리즘을 사용할 수 있다.
다수의 소수 판별
- 에라토스테네스의 체 알고리즘을 사용한다.
에라토스테네스의 체(Sieve of Eratosthenes) 란?
고대 수학자 에라토스테네스가 만들어 낸 소수를 찾는 방법이다.
이 방법은 체로 치듯이 수를 걸러낸다고 해서 '에라토스테네스의 체'라고 불린다.
소수를 구하는 방법은 여러 가지가 존재하지만 이 방식을 이용하면 보다 효과적으로 소수를 빠르게 구할 수 있다.
에라토스테네스의 체 알고리즘
- 다수의 자연수에 대하여 소수 여부를 판별할 때 사용하는 대표적인 알고리즘이다.
- 에라토스테네스의 체는 N보다 작거나 같은 모든 소수를 찾을 때 사용할 수 있다.
- 에라토스테네스의 체 알고리즘의 구체적인 동작 과정은 다음과 같다.
- 2부터까지의 모든 자연수를 나열한다.
- 남은 수 중에서 아직 처리하지 않은 가장 작은 수 𝑖를 찾는다.
- 남은 수 중에서 i의 배수를 모두 제거한다.(𝑖는 제거하지 않는다.)
- 더 이상 반복할 수 없을 때까지 2번과 3번의 과정을 반복한다.
에라토스테네스의 체 알고리즘 동작 예시
- [초기 단계] 2부터 26까지의 모든 자연수를 나열한다 (𝑁 = 26)
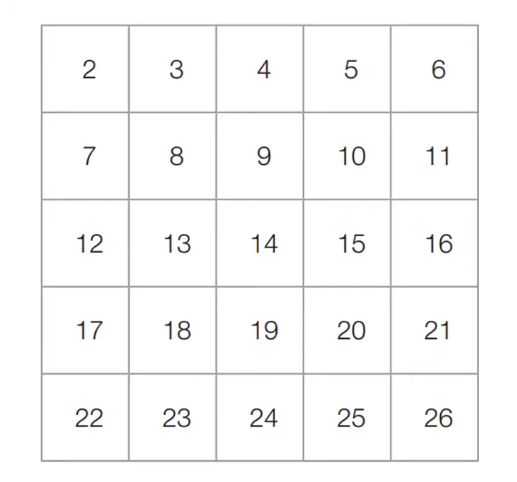
- [Step 1] 아직 처리하지 않은 가장 작은 수 2를 제외한 2의 배수는 모두 제거한다

- [Step 2] 아직 처리하지 않은 가장 작은 수 3을 제외한 3의 배수는 모두 제거한다
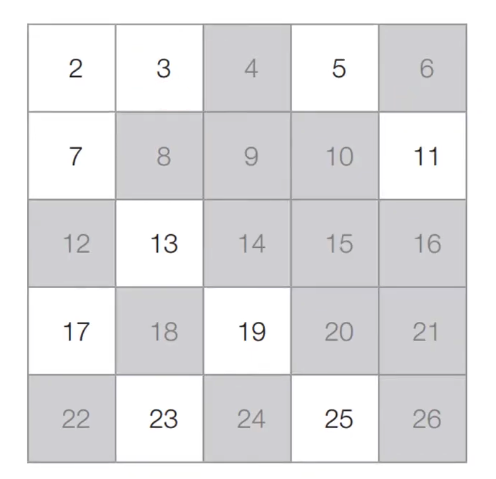
- [Step 3] 아직 처리하지 않은 가장 작은 수 5를 제외한 5의 배수는 모두 제거한다

- [Step 4] 마찬가지의 과정을 반복했을 때 최종적인 결과는 다음과 같다

소수의 판별: 에라토스테네스의 체 알고리즘
1. 에라토스테네스의 체 알고리즘 소스 코드 : 파이썬 (Python)
import math
n = 1000 # 2부터 1,000까지의 모든 수에 대하여 소수 판별
# 처음엔 모든 수가 소수(True)인 것으로 초기화(0과 1은 제외)
array = [True for i in range(n + 1)]
# 에라토스테네스의 체 알고리즘 수행
# 2부터 n의 제곱근까지의 모든 수를 확인하며
for i in range(2, int(math.sqrt(n)) + 1):
if array[i] == True: # i가 소수인 경우(남은 수인 경우)
# i를 제외한 i의 모든 배수를 지우기
j = 2
while i * j <= n:
array[i * j] = False
j += 1
# 모든 소수 출력
for i in range(2, n + 1):
if array[i]:
print(i, end=' ')
2. 에라토스테네스의 체 알고리즘 성능 분석
- 에라토스테네스의 체 알고리즘의 시간 복잡도는 사실상 선형 시간에 가까울 정도로 매우 빠르다.
- 시간 복잡도는 O(NloglogN) 이다.
- 에라토스테네스의 체 알고리즘은 다수의 소수를 찾아야 하는 문제에서 효과적으로 사용될 수 있다.
- 하지만 각 자연수에 대한 소수 여부를 저장해야 하므로 메모리가 많이 필요하다.
- 10억이 소수인지 아닌지 판별해야 할 때 에라토스테네스의 체를 사용할 수 있을까?
경우에 따라서는 메모리 측면에서 매우 비효율적으로 동작할 수 있다.
시간 복잡도 추가 설명
에라토스테네스의 체 알고리즘의 시간 복잡도는 O(NloglogN)으로 사실상 선형 시간에 동작할 정도로 빠르다.
N이 1,000,000이라고 하면 NloglogN은 약 4,000,000 정도이다.
다만, 메모리가 많이 필요하다는 단점이 있다. 알고리즘을 수행할 때 N의 크기만큼 리스트를 할당해야 하기 때문이다.
예를 들어 N = 1,000,000일 때는 2부터 1,000,000까지의 모든 수에 대한 정보를 담을 수 있는 크기의 리스트가 필요하다. 또한 10억이 소수인지 찾는 문제에서는 에라토스테네스의 체를 이용하기 어렵다.
따라서, 에라토스테네스의 체를 이용해야 되는 문제의 경우 N이 1,000,000 이내로 주어지는 경우가 많다.
그렇게 하면 이론상 400만 번 정도의 연산으로 문제를 해결할 수 있으며, 메모리 또한 충분히 처리할 수 있는 크기만큼만 차지하게 된다.
예시를 통한 설명 (에라토스테네스의 체 알고리즘)
에라토스테네스의 체 원리, 사용 방법, 알고리즘
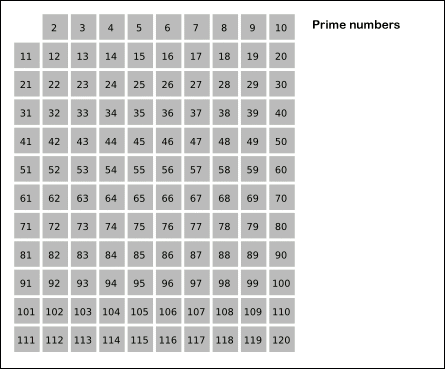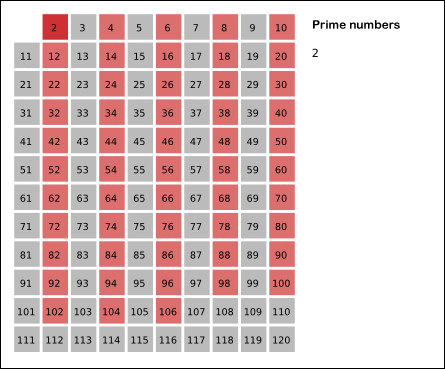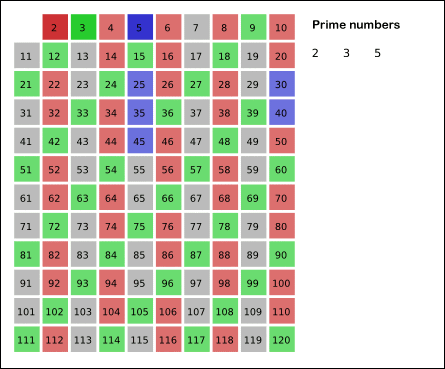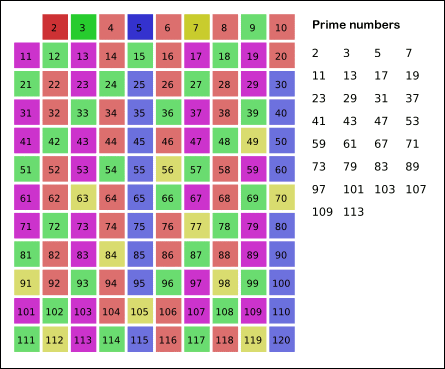
간단히 위 그림을 설명하자면 1과, 2, 3, 5, 7의 배수인 수들을 모두 제거하면 소수만 남게 된다.
어떻게 이런 방식을 사용할 수 있을까?라는 질문이 나올 수 있다.
우선 소수에 대해 알아볼 필요가 있다.
소수란 1과 자기 자신 이외에 약수를 가지는 합성수이다. 그렇다면 여기서 위의 원리를 유추할 수 있다.
즉 1과 자기 자신 이외에 약수를 가지게 되는 경우를 제거해야 소수가 되기 때문에
1을 예외로 제거하고 2, 3, 5, 7의 배수를 제거하면 결국 남는 건 소수뿐이다라는 것을 알 수 있다.
그림의 경우, 11*11 > 120 이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수다.
자세한 ( 알고리즘 진행 방식 )은 아래와 같다.
1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
참고자료
https://gururuglasses.tistory.com/80
https://freedeveloper.tistory.com/392
'Algorithm' 카테고리의 다른 글
| [알고리즘] 서로소 집합 (Disjoint Sets) - 사이클 판별 (0) | 2023.12.10 |
|---|---|
| [알고리즘] 서로소 집합 (Disjoint Sets) - 자료구조 (0) | 2023.12.09 |
| [알고리즘] 최장 증가 부분 수열(LIS) 알고리즘 (0) | 2023.09.01 |
| [알고리즘] 이진 탐색 / 이분 탐색 (Binary Search) (0) | 2023.08.17 |
| [알고리즘] 시간 복잡도 (Time Complexity) (0) | 2023.08.14 |